Interpretation of the Average High Water line from air photography: variability and repeatability
Richard C. Daniels, Peter Ruggiero, and
Diana McCandless
Washington Department of Ecology
INTRODUCTION
As part of the Southwest Washington Coastal Erosion Study detailed shoreline change analyses are being conducted. These analyses are dependent on shorelines derived from historical maps, orthophotography, GPS ground survey, and airborne Light Detection and Ranging (LIDAR) systems. Each of these methods may be used to estimate the location of the average high water line (AHWL). Each method has its own strength and weakness. For example, National Ocean Service (NOS) used ground surveys to derive the AHWL for their 1880 era and 1926 era topographic sheets (T-Sheet) and air photography for their 1950 era sheets. The Department of Ecology is digitizing shorelines from orthophotos using visual queues that are equivalent to those used by NOS (Shalowitz 1964). To confirm this assertion, tests were conducted in 1998 in which four air photos used for a 1950 era NOS T-Sheet were obtained, scanned, and orthorectified by Ecology. The AHWL was digitizing from these orthophotos and compared to the 1950 era NOS T-Sheet. The lines were almost identical.
This initial attempt at determining the homogeneity of an interpreted AHWL brought to light the need to conduct a detailed shoreline extraction, shoreline repeatability, and a shoreline variability experiment. The information produced by each analysis provides the basic information needed to develop a detailed error budget for the average high water lines derived by the study.
Shoreline Extraction
NOS T-Sheets are the only readily available data source to obtain information on shoreline position prior to 1940 (i.e., the advent of organized regional air photo missions by state and federal governments). T-sheets are detailed records of surveys that were conducted to provide coastlines for use on navigation charts issued by NOS (formerly the U.S. Coast and Geodetic Survey).
The National Oceanic and Atmospheric Administration (NOAA) has undertaken a data rescue project to convert historical T-sheets from paper to a digital format. NOAA has partnered with several state agencies across the nation to assist in extracting the line work (and assigning attribute information) from the raster images into vector data sets.
As the coastal zone management agency for the state of Washington, the Department of Ecology has undertaken the task of digitizing shorelines for Washington and the northwest ocean coast of Oregon from the raster images and saving them into digital vector files. To complete the quantitative analysis of shoreline change, it was essential that we quantify the accuracy of the processes used to extract the shorelines from the historical T-sheets.
A detailed accuracy assessment was conducted on the methods used to extract the NOS AHWL from the NOS T-Sheets. The results of this analysis are described in detail in Daniels and Huxford, 1999. In summary, the analysis determined:
The vector data obtained from the 1950 era T-sheets meets published NOS accuracy standards for the original data source (±3 m (9.8 ft) for 1:10,000 T-sheet to ±6 m (19.6 ft) for 1:20,000 T-sheets). The 1926/27 era T-sheets are slightly less accurate, yet still meet the 1950 era accuracy standards. A majority of the error in the 1926/27 T-sheets has been associated with the datum transformation process (i.e., between the North American Datum, North American Datum of 1927, and North American Datum of 1983).
Shoreline Repeatability
The strength of orthorectified air photography is that it provides context and visual queues that assist in identifying the AHWL. However, one of the initial concerns of the study was that interpreted location of the AHWL would vary significantly based on the skill level of the staff member and due to changing interpretations of the contextual information in the photo. These two error sources were addressed early on in the study. Firstly, the same individual was assigned the task of digitizing all shorelines from the orthophotography. Secondly, a detailed description of the visual queues that should be used to identify the shoreline reference feature (a.k.a., AHWL) and the erosion reference feature (a.k.a., vegetation or scarp line) were developed and are as follows:
The shoreline change reference feature (SCRF) will be the average high water line (AHWL). This line is estimated based on the dewatering line and drift line. In general, this line is about 5 to 10 m landward of the darker beach sand, which was wetted by wave run-up within hours of the photo being taken. In a few cases this line will not be visible because:
- photo taken just prior to, or after, high tide;
- angle from ground to camera was such that high reflectance values mask the difference in shading;
- SCRF is located at a bluff, cliff, or scarp.
Even with these precautions, the need to quantify the variability in the AHWL delineation processes remained. To address this, a shoreline repeatability study was designed to look at two different factors.
The experiment design utilized photos of four locations from within the Columbia River Littoral Cell (CRLC) cover 18 kilometers of shoreline. Black and white diapositives and prints were obtained for each site. These photos were scanned at 600 dpi and orthorectified using the same control points for each media type to obtain orthorectified photos with cell sizes of 0.5 by 0.5 m. Locational differences between each version of the identical images was ±1 pixel (0.5 m).
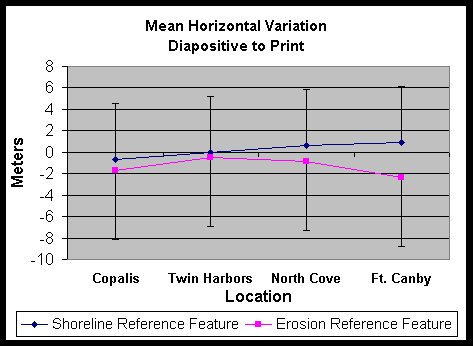
The print/diapositive pairs were presented in random order at three different sittings to the data analyst who was required to digitize the AHWL and vegetation line on each image. To minimize the ability of the analyst to "remember" what they had digitized in the past, the analyst was required to wait 24 hours before digitizing the next set. The difference between the digitized shorelines was calculated used the change rate program used by the study (Daniels 1998) and are shown in Figure 1.
The diapositive to print analysis obtained a mean difference in location of the AHWL of 0.22 m with a standard deviation of 5.22 m over the 18 km’s sampled. The print to print analysis, which was conducted for a single photo with 3.5 km of shoreline, obtained a mean difference of 0.22 m and a standard deviation of 1.11 m. In contrast, the diapositive to print analysis for this same photo obtained a mean of 0.9 m and a standard deviation of1.2 m. Thus, the between sample standard deviation is larger than the between media type variation. This indicates that the less expensive prints (~$2 vs. $12 for diapositives) are suitable for delineating the AHWL.
To look at the potential impact of a different analyst digitizing the photos, a second analyst digitized the shoreline and vegetation line for each image. The results of this analysis are shown in Figure 2. Specifically, the interpretation of the vegetation line had a mean difference of 2.83 m and a standard deviation of 9.11 m. The interpretation of the AHWL varied by a larger amount, in this case the mean difference was 12.44 m with a standard deviation of 8.76 m –the second analyst consistently digitized a line about 10 m further seaward than the first.
Shoreline Variability
A limitation of the photographic method is that the digitized AHWL is estimated for a single point in time based evidence visible in the photo from the last two high tides. Thus, the AHWL is not based on a long-term record of tide levels as implied by the name. The term mean high water, as used when discussing tide gauge data, implies a fixed elevation that has been calculated based on a long term gauge record. Thus, the digitized AHWL does not represent the line that would be calculated if the MHW for a region were used in combination with an elevation model of the beach. However, it is impossible to quantify the difference between the two unless a topographic survey is conducted during, or directly following, the air photo mission.
There are limitations with the use of context free topographic surveys as well. On the ocean coast the AHWL is influenced by several factors in addition to tide levels. These factors include wave height and wave run-up; both serve to place the AHWL further landward than it would be location if it were surveyed using traditional spirit levels or GPS technology, since one would survey a MHW elevation as derived from a tide gauge.
Several tests were conducted to quantify the variability associated with using an AHWL from a single photo as a surrogate for the mean high water line for an entire season or year. These tests required the following data collection and creation activities:
Based in this data the following analyses were conducted.
Figure 3 provides a graphical representation of how the two-dimensional (GPS vs. photo derived AHWL) and the three-dimensional (elevations) parts of this analysis interact.
Preliminary results from this experiment are shown in Figures 4 through 7.In Figure 4 and 5 one can see that the interpreted AHWL and AHHWL closely coincides with the AHWL digitized from the orthophotography. In both May and September the AHWL and AHHWL interpreted on the ground during the GPS surveys were, on average, within 12.5 m of the digitized AHWL. Figures 6 and 7 shows the relationship between true elevations (in this case NAVD 88 meters) and the digitized AHWL. The digitized AHWLs were overlaid on top of topographic surfaces and the elevation extracted for every 10 m along the line. The May overlay obtained a mean NAVD 88 elevation for the line of 2.68 m with a standard deviation of 0.14 m. The September overlay obtained a mean NAVD88 elevation for the line of 2.98 m with a standard deviation of 0.08 m.
The change rate program utilized in the shoreline repeatability analysis (Daniels and Huxford 1989) was used here also. This analysis found that the digitized AHWL receded on average 10 m from May to September (Standard Deviation 7.31 m). During a period that seaward movement of the shoreline would be expected.
RESULTS
This three-part analysis was designed to obtain a detailed error budget for all components that enter into the calculation of shoreline change rates for the Southwest Washington Coastal Erosion Study. Initial findings are as follows:
CONCLUSIONS
The interpreted AHWL from both the orthophotos and NOS T-Sheets provides shorelines that are accurate to ±12 m or better. However, seasonal variability in the size and location of nearshore sand bars and changes in the beach slope from spring to fall resulted in a change in the wave run-up characteristics on the beach. These changes have manifests themselves by changing the elevation of the AHWL. Thus, the AHWL does not have a fixed value but, in this study, varied from 2.7 m to 3.0 m during the transition period from spring to fall under. Note that the AHWL was obtained from photos or charts on days with "average weather conditions" –where average conditions are characterized by winds of less than 10 knots, mean wave heights (Hs) of less than 2 m, and tide levels between 1 and 2 m MLLW.
The elevation variability described above translated into an AHWL that may migrate as much as 41 m during the transition from summer to fall. This natural variation, when combined with the uncertainty associated with the photo derived AHWL, indicates that the interpreted location of the AHWL could vary as much as ±23 m from May to September.
If taken at face value, the range of potential AHWL locations during a single Spring-Fall season results in large uncertainty value. When comparing shorelines from two different years, this uncertainty estimate would mask all but the largest changes in shoreline position. Traditionally, uncertainty values are seen as additive terms (e.g., ±5 for each shoreline plus the horizontal variability of the potential AHWL for each year). The additive method results in an uncertainty term of ±34 m for two AHWLs obtained from photos taken on two different years in the month of May. If we assume that these photos were taken ten years apart, the change rates need to be less than –3.4 m or greater than 3.4 m per year to be significant.
However, if we explicitly consider of the month in which the AHWL was obtain in calculating our uncertainty value, we may view the uncertainty related to natural variability in the position of the AHWL within a single month as a singular term. This would reduce our uncertainty value in the above scenario to ±23 m. This reduces the size of our critical change rate, and would make change values of less than -2.4 m or greater than 2.4 m significant. Table 1 contains an estimate of the average monthly variability of the AHWL for the months of May to September and shows the critical change rate values based on a ten-year and twenty-year time period between photos. These ranges assume that the AHWL was digitized under "average conditions" and that the physical state of the beach in May 1999 and September 1999 was representative of the average condition of the beach for those months over some multi-year time period.
Table 1. Estimate of the average monthly variability of the AHWL for the months of May to September and shows the critical change rate values based on a ten-year and twenty-year time period between photos.
| Shoreline | Beach | AHWL | AHWL (Photo) | Total | Critical Change Rate | |
| Month | Slope | Variability | Repeatability | Uncertainty | 10 Years | 20 Years |
| May | 2.30% |
13.0 |
5 |
23.0 |
2.3 |
1.2 |
| June | 2.15% |
14.0 |
5 |
24.0 |
2.4 |
1.2 |
| July | 2.00% |
15.0 |
5 |
25.0 |
2.5 |
1.3 |
| August | 1.85% |
16.2 |
5 |
26.2 |
2.6 |
1.3 |
| September | 1.70% |
17.6 |
5 |
27.6 |
2.8 |
1.4 |
REFERENCES
Daniels, R.C. and Huxford, R.H. In press. An Error Assessment of Vector Data Derived from Scanned NOAA, Topographic Sheets. Journal of Coastal Research
Daniels, R.C. and R. H. Huxford. 1998. Coastline Mapping and Identification of Erosion Hazard Areas in Pacific County, Washington. In 1998 ESRI International User Conference Proceedings. ESRI, Redlands, CA.
Huxford, R.H. and Daniels, R.C. 1998. Historical map recovery using multiple integrated ESRI programs. ESRI Eighteenth Annual User Conference Proceedings, ESRI, Redlands, CA.
Schalowitz, A.L. 1964. Shoreline and Sea Boundaries, Volume 2. U.S. Department of Commerce, Coast and Geodetic Survey, Washington, DC.
FIGURES
Figure 1. Mean variation between the repeated interpretation of the average high water line for four locations within the Columbia River Littoral Cell.

Figure 2. Mean difference between the interpreted average high water line digitized by two different analysts for four locations within the Columbia River Littoral Cell.
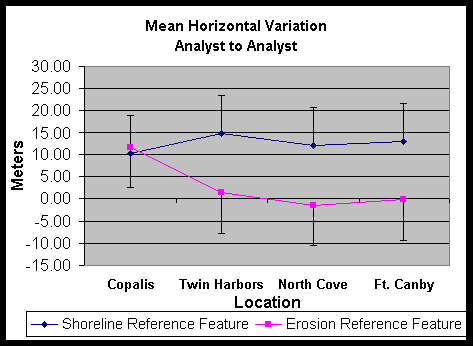
Figure 4. Comparison of a photo derived AHWL for May 26, 1999 with an AHWL and AHHWL obtained from ground survey taken one day after the flight.
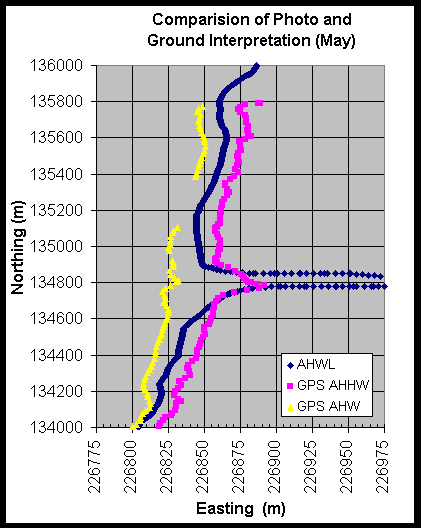
Figure 5. Comparison of a photo derived AHWL for September 21, 1999 with an AHWL and AHHWL obtained from ground survey taken three days after the flight.
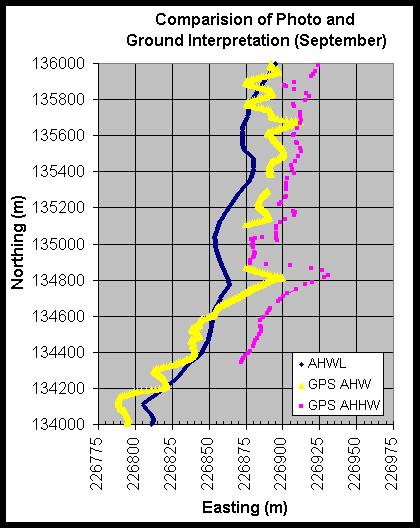
Figure 6. Comparison of GPS derived two and three meter contours with the digitized AHWL for May 26, 1999. Mean AHWL elevation is 2.68 m.
Figure 7. Comparison of GPS derived two and three meter contours with the digitized AHWL for September 21, 1999. Mean AHWL elevation is 2.98 m.